Why are Polynomials and Importance in Mathematics?

Mathematics is the study of measuring physical quantities in terms of numbers and space and analyzing it into understandable form to make our complicated tasks easy. Mathematics is basically a Greek word which means propensities to learn and there are many associated branches of it which are extensively used in science and are related to numbers including algebra, calculus, geometry, probability, etc. Mathematics plays a vital role in various sectors of life, which could be time tracking, finance, banking, engineering, medical, accounting, software, etc. All these aspects require a fundamental mathematical background to analyze and decode it into simpler forms rather than using cumbersome methods.
Mathematics is one of the most powerful and versatile tool one can use for rational understanding and organizing daily cumbersome problems. With the use of mathematics, we develop modelling of physical forms into equations and hence make it logical to break down its chaos. Math have been very affective in abstract or spatial thinking as well even effective in communication skills. It encourages logical reasoning, critical as well creative thinking ability. In a nutshell mathematics is the fundamental way of all creations, without which our problems in various aspects of life cannot be reached, analyzed as well as developed in optimum level. Here one such section or part of the mathematics we are going to discuss with its importance in mathematics which is none other than polynomials. It is the most common word that every one encounters while studying mathematics and so its significance has in this subject. Well, it is way beyond that. In mathematics, a polynomial is basically a expression form which mainly constitutes variables which also known as indeterminates and coefficients associated with it, and they are altogether operated by mathematical operators like addition, subtraction, multiplication, and positive integer exponential function of variables. For example, a typical single variable polynomial could be: x2+9x -3, here variable is x. Similarly, an example of three variable polynomials could be: x3 – 2yz2 − xz – 9.
Polynomial have significant uses in many branches and sections of mathematics and science. The real-life physical problems can be converted into polynomial form of equations, which encapsulate a wide range of parameters which are dependent on the problem and can give a suitable result. Considering any problem from basic physics or chemistry to economics or accounts polynomial function can be used to express the variable parameter in form of its dependence with respect to the variation.
Thus, it can be said that a polynomial is mathematical form of expression involving various relevant dependent constants and variables which also known as indeterminants that are operated by addition, subtraction, multiplication and positive integer power exponentials. General form of single variable x polynomial can be written in format as given below:
Where a0, a1, a3,…. are the constants and x being variable. Though x represents no value, but any value may be substituted in it. The mapping involves the result of this substitution to the value of function, called polynomial function.
Using the summing notation, it can be expressed as:
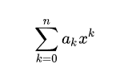
Therefore, a polynomial can be zero, or can be expressed as the sum of number of non-zero values. Each term of a polynomial function has product number which is called as the coefficient of a particular term. The exponent or power associated with the variable or indeterminate is called as the degree of a polynomial. Also, if the polynomial function consists of two or more indeterminates then the sum of the power or exponents will be the degree of the polynomial function. For example -8x3y2 is a term. Here the coefficient of above term is -8, the variables are x and y, the degree of x is 3 and degree of that of y is 2. The degree of the entire term will be the sum of degrees of each of variables in the term, so in above degree will be 3+2=5. Polynomial having one variable if has degree one then called as linear polynomial, for degree 2 called quadratic polynomial, for degree 3 called as cubic polynomial. Also, there are different kinds of polynomial function i.e., it is categorized in various types such as constant polynomial, zero polynomial, homogenous polynomial, real polynomial, complex polynomial and multivariate polynomial.
- The one which has no terms in it can be called as zero polynomial.
- A polynomial is referred as a homogenous polynomial if all the variables have the degree n.
- The polynomials have only real coefficients are called as real polynomials and similarly those having complex coefficients called a complex polynomial.
- The polynomial consisting more than one variable are called as multivariate polynomials.
Polynomials are widely used in interpolation and approximation of solving complex and large equations using numerical techniques and can be used to represent information about some other object. The characteristic polynomial of a matrix having linear operators contains information about the eigen values of the operator. Every polynomial P in x defines x-> P(x), called polynomial function of P, the equation P(x)=0 is polynomial equation influenced by P. The roots of the polynomial equations are determined by solutions of this equation or the zeros of the associated function. Hence polynomial is most important building block of mathematics.
Do you know: The zeros of the polynomial x^ (2) – 2x-3 are?
Visit for more website: forbesblog.org